March Madness

library(tidyverse) # ggplot, lubridate, dplyr, stringr, readr...
library(praise)

The Data

March is NCAA basketball March Madness! This week’s data is NCAA Men’s March Madness data from Nishaan Amin’s Kaggle dataset and analysis Bracketology: predicting March Madness.

team_results <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2024/2024-03-26/team-results.csv')
public_picks <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2024/2024-03-26/public-picks.csv')

Team performance

Caveat: some of the variables were a little difficult for me to parse. I’m not sure what “performance against” means in the PAKE and PASE variables. And at first we were looking at schools with different PAKE and PASE. But later we thought it might be more interesting to look at schools whose PAKE and PASE were both high (or low).

seed_data <- team_results |>
  mutate(expectations = ifelse(PAKE >= PASE, "underseeded", "overseeded")) |>
  mutate(rank_diff = PAKE-PASE) |>
  #filter(abs(PAKE - PASE) > 1) |>
  mutate(expect_grps = case_when(
    PAKE - PASE < -2 ~ "way_under",
    PAKE - PASE < -1 ~ "little_under",
    PAKE - PASE < 0 ~ "under",
    PAKE - PASE < 1 ~ "over",
    PAKE - PASE < 2 ~ "little_over",
    TRUE ~ "way_over")
    ) |>
  mutate(expect_grps = factor(expect_grps, 
                              levels = c("way_under", "little_under","under", "over",
                                         "little_over", "way_over")))

seed_data |>
  ggplot(aes(x = PAKE, y = PASE, color = expect_grps)) + 
  geom_point() + 
  geom_abline(slope = 1, intercept = 0) +
  labs(x = "Performance against Komputer ranking", y = "Performance against seed ranking", color = "expected groups") +
  scale_color_manual(values = c("red", "orange", "yellow", "lightblue", "blue", "purple")) + 
  ggrepel::geom_label_repel(data = filter(seed_data, abs(PAKE-PASE) > 1.5), mapping = aes(label = TEAM), key_glyph = "point") +
  guides(color = guide_legend(override.aes = list(size = 3)))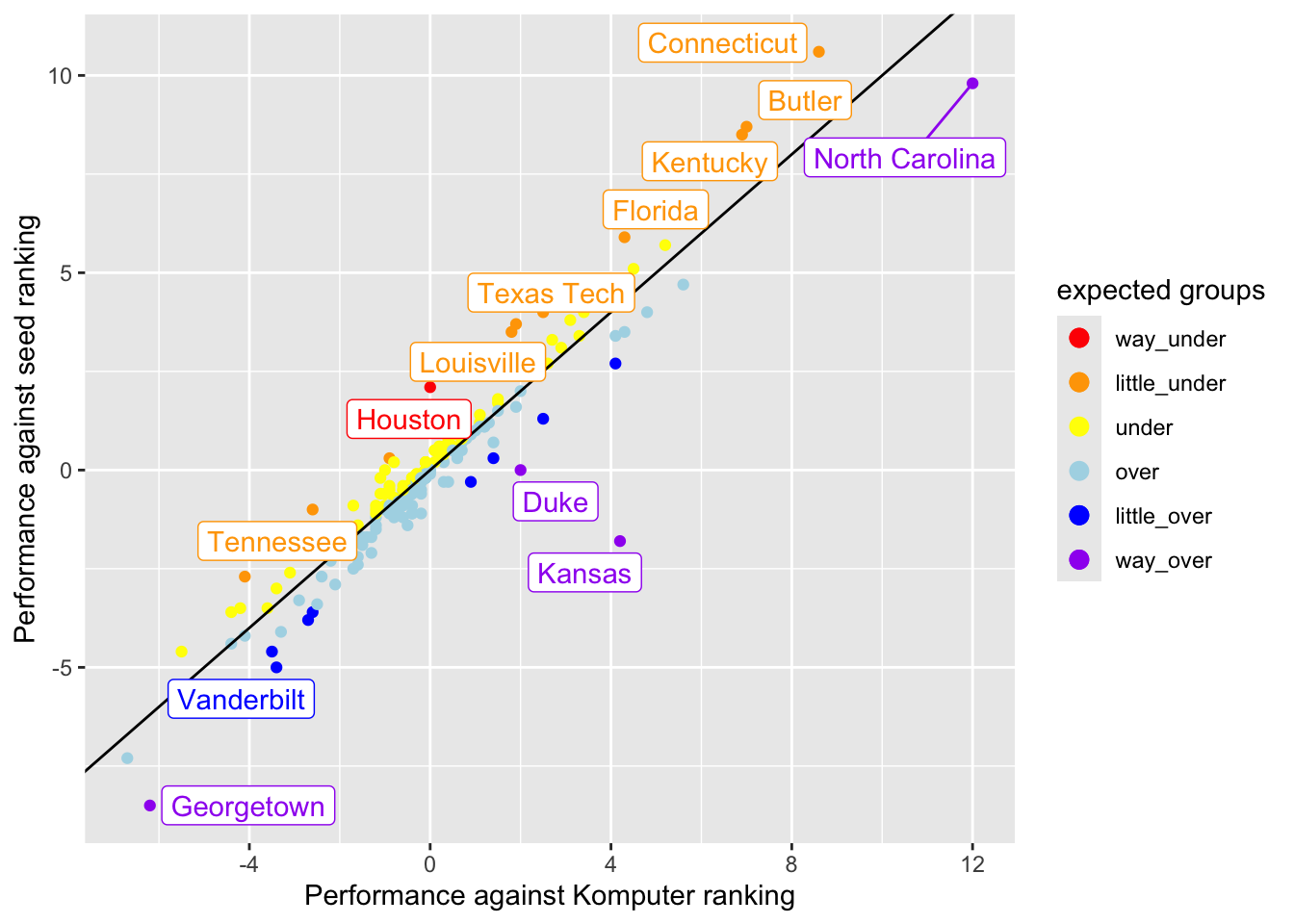

Scatter plot to show the difference between PAKE and PASE. The colors represent how different PAKE and PASE are. However, maybe it makes more sense to look at schools in the upper corner or lower corner.

library(ggradar)

team_results |>
  mutate(F4PERCENT = parse_number(F4PERCENT)) |>
  select(TEAM, PAKE, PASE, GAMES, W, R64, F4PERCENT) |>
  mutate(across(PAKE:F4PERCENT, scale)) |>
  filter(TEAM %in% c( "Houston", "Butler", "Florida Atlantic", "Kansas", "Purdue")) 

# A tibble: 5 × 7
  TEAM             PAKE[,1] PASE[,1] GAMES[,1]     W[,1] R64[,1] F4PERCENT[,1]
  <chr>               <dbl>    <dbl>     <dbl>     <dbl>   <dbl>         <dbl>
1 Butler            3.17       3.69      1.75   1.76       1.43          0.839
2 Florida Atlantic  1.49       1.44     -0.293 -0.000574  -0.892        -0.466
3 Houston           0.00421    0.892     0.973  1.08       0.562         2.39 
4 Kansas            1.90      -0.764     4.38   4.88       3.18          3.19 
5 Purdue           -1.98      -1.87      2.05   1.63       2.60          2.30 

team_results |>
  mutate(F4PERCENT = parse_number(F4PERCENT)) |>
  select(TEAM, F4PERCENT, PAKE, PASE, GAMES, W, R64) |>
  mutate(across(F4PERCENT:R64, scale)) |>
  filter(TEAM %in% c("Houston", "Butler", "Florida Atlantic", "Kansas", "Purdue")) |>
ggradar(values.radar = c("-4", "0", "4"),
        grid.min = -2, grid.mid = 0, grid.max = 5,
        group.line.width = 1,
        group.point.size = 2)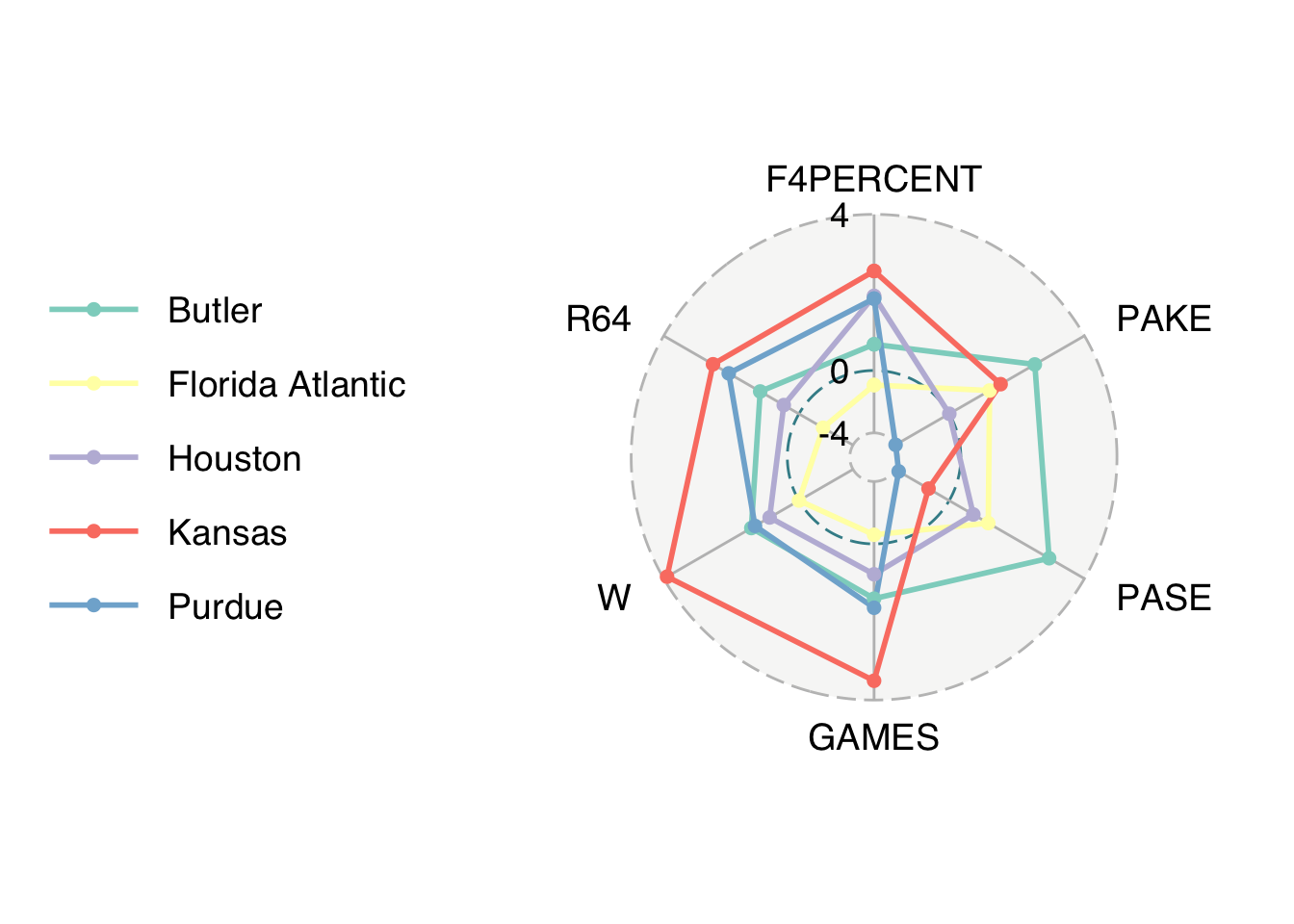

Radar plot on the following variables: times making it to the final 4 percent, PAKE, PASE, number of games played in the tournament, number of wins in the tournament, and number of times to the round of 64. Using different variables, we can see if schools perform high on one variable and low on another. Given that the variables are all on different scales, we created z-scores for each of the variables before plotting them on the radar.

praise()

[1] "You are great!"